Sorodno iz bloga

Linearna funkcija
05.06.2024 | Matematika

Naravna števila
23.01.2020 | Matematika
Elipsa
20.12.2019 | Matematika
Deli na družabnih omrežjih

05.06.2024 | Matematika
 Linearna funkcija je ena najosnovnejših funkcij v matematiki – povejmo po domače: če imamo v koordinatnem sistemu neskončno točk, ki vse ležijo na isti premici, lahko vse te točke naekrat povzamemo oziroma predstavimo s predpisom linearne funkcije. (No, edino navpičnih premic ne moremo tako predstaviti, ampak tudi ta problem so matematiki rešili. So brihtne glavce, saj vem.)
Linearna funkcija je ena najosnovnejših funkcij v matematiki – povejmo po domače: če imamo v koordinatnem sistemu neskončno točk, ki vse ležijo na isti premici, lahko vse te točke naekrat povzamemo oziroma predstavimo s predpisom linearne funkcije. (No, edino navpičnih premic ne moremo tako predstaviti, ampak tudi ta problem so matematiki rešili. So brihtne glavce, saj vem.)
Linearna funkcija ima predpis ![]() je enak
je enak ![]() , kjer sta
, kjer sta ![]() in
in ![]() neki realni števili. Ravno vrednosti teh dveh števil
neki realni števili. Ravno vrednosti teh dveh števil ![]() in
in ![]() določata, katera premica opisuje te točke. Zapis neskončnega števila točk smo tako zreducirali na dve vrednosti,
določata, katera premica opisuje te točke. Zapis neskončnega števila točk smo tako zreducirali na dve vrednosti, ![]() in
in ![]() . Impresivno, kajne?
. Impresivno, kajne?
Še več, matematiki so odkrili, da števili ![]() in
in ![]() v sebi nosita informacijo, kako ta premica izgleda! Število
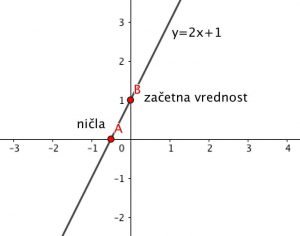
v sebi nosita informacijo, kako ta premica izgleda! Število ![]() je smerni koeficient, ki določa strmino premice. Število
je smerni koeficient, ki določa strmino premice. Število ![]() pa imenujemo začetna vrednost in nam pove, kje premica seka
pa imenujemo začetna vrednost in nam pove, kje premica seka ![]() os. In ne samo to!
os. In ne samo to!
Matematiki so ugotovili so tudi, da:

Če imamo podani dve točki na grafu linearne funkcije, npr. ![]() in
in ![]() , lahko
, lahko ![]() izračunamo s spodnjo formulo:
izračunamo s spodnjo formulo:
![]()
Ker pa so matematiki radovedne sorte, so si postavili še cel kup drugih vprašanj. Kje premica seka ![]() os (kje namreč seka
os (kje namreč seka ![]() os smo že ugotovili — poglej gor) ali pa pod kakšnim kotom premica narašča oz. pada? Sami številki
os smo že ugotovili — poglej gor) ali pa pod kakšnim kotom premica narašča oz. pada? Sami številki ![]() in
in ![]() nam tega ne znata direktno povedati. Do odgovora pridemo, če znamo predpis funkcije pravilno uporabiti.
nam tega ne znata direktno povedati. Do odgovora pridemo, če znamo predpis funkcije pravilno uporabiti.
Poglejmo najprej, kako izračunamo, kje linearna funkcija ![]() seka
seka ![]() os. Na grafu je to točka
os. Na grafu je to točka ![]() , kar pomeni, da mora veljati
, kar pomeni, da mora veljati
![]()
Rešitev te enačbe nam pove, kje graf linearne funkcije seka ![]() os.
os.
Temu rečemo tudi ničla funkcije.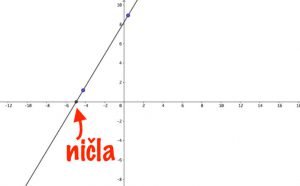
Glede naklonskega kota ![]() premice, ki je predstavljena s predpisom
premice, ki je predstavljena s predpisom ![]() , pa velja
, pa velja
![]()
Zanimivo, kako se vse tako lepo izide!
Ker matematikom še ni bilo dovolj, so raziskovali dalje in ugotovili, da lahko enačbo premice zapišejo na tri različne načine. Recimo, da imamo premico, ki jo predstavimo kot graf linearne funkcije ![]() . Prva možna oblika za enačbo premice je najbolj enostavna:
. Prva možna oblika za enačbo premice je najbolj enostavna: ![]() zamenjamo z
zamenjamo z ![]() in dobimo:
in dobimo:
![]()
Pa so se matematiki igrali naprej in prišli do naslednje oblike:
![]()
Ta oblika jim je navse ljuba, saj lahko predstavlja tudi navpične premice, ki jih prva ne more. Potem pa obstaja še tretja, ki je namenjena še posebej lenim matematikom, saj je iz nje najlažje narisati premico v koordinatni sistem. Izleda pa takole:
![]()
Da so se lahko matematiki o vseh teh treh oblikah pogovarjali, si izmenjevali trače in zgodbe, so vsako od njih poimenovali. Tako kot starši poimenujejo svoje otroke, da se lahko potem pred sosedom pohvalijo, kako je
“Peter danes sestavil domiseln indijanski šotor iz bobi palčk!”
Poimenovanje gre takole:
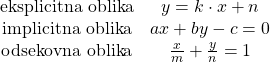
Če te zanima, kako preoblikuješ eno obliko v drugo, si poglej še naš spodnji video posnetek.
Enačbo ![]() preoblikuj v implicitno in odsekovno obliko.
preoblikuj v implicitno in odsekovno obliko.
Ne boste verjeli, ampak matematikom še ni bilo dovolj. Zanimalo jih je, kaj vse lahko izračunajo, če imajo dve premici! Ne bomo komentirali, kajne?
Ugotovili smo, da lahko iz smernih koeficientov zelo hitro ugotovimo, če sta premici vzporedni ali če sta pravokotni. Če imamo npr. dve premici, ena ima enačbo ![]() , druga pa
, druga pa ![]() , velja, da:
, velja, da:
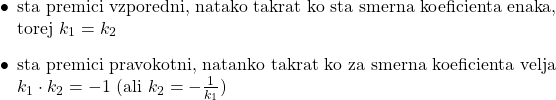
Izračunamo lahko njuno presečišče, ki je vedno ena točka, razen če sta premici vzporedni (v tem primeru presečišča ni). Koordinate točke dobimo tako, da rešimo sistem enačb, ki predstavljata premici. Kako točno to izleda v praksi, si poglej v video posnetku.
Pa da ne pozabimo še na kot! Pod kakšnim kotom se sekata, če nista vzporedni? Tudi na to so našli odgovor, in sicer za kot ![]() med premicama velja
med premicama velja ![]()
Nariši graf linearne fukcije ![]()
Iz predpisa razberi, ali bo premica naraščala ali padala ter to utemelji.
Zapiši enačbo premice in začetno vrednost.
Izračunaj ničlo.
Zapiši enačbo premice, ki gre skozi točko ![]() in je vzporedna premici z enačbo
in je vzporedna premici z enačbo ![]()
Vzporedni premici imata enak smerni koeficient. Izračunamo ga tako, da enačbo premice ![]() preoblikujemo v eksplicitno obliko. Enačba iskane premice je potem enaka
preoblikujemo v eksplicitno obliko. Enačba iskane premice je potem enaka ![]() . Izračunati moramo še začetno vrednost. To naredimo tako, da v to enačbo vstavimo točko A in izračunamo n.
. Izračunati moramo še začetno vrednost. To naredimo tako, da v to enačbo vstavimo točko A in izračunamo n.
Če te v zvezi s snovjo Linearna funkcija še karkoli zanima ali pa potrebuješ pomoč pri učenju, pridi na inštrukcije matematike, kjer ti z veseljem pomagamo, da poglobiš svoje znanje.
Deli na družabnih omrežjih
Prijavi se na e-novice
Sorodno iz bloga

05.06.2024 | Matematika

23.01.2020 | Matematika

20.12.2019 | Matematika
Si iz pravega testa za inštruktorja?
Povej več o sebi tukaj.
041 926 000
Horizont d.o.o.
(SI65826736)
Pohlinova ulica 20
1000 Ljubljana